/ Examples / Control / Tempo

Wherein we entertain deep questions on the constancy of time.

Right-click to copy this example to your workspace

Overview

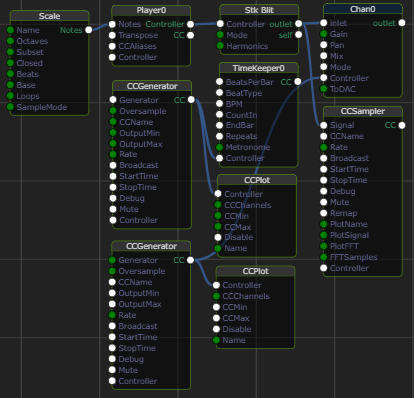
At the heart of this example are two CCGenerator nodes. The top one is connected to TimeKeeper0 and the bottom one feeds values into Chan0. The CC values produced by these nodes are also routed to CCPlot nodes to enhance your understanding of the signals in play. For the icing on the cake we also employ a CCSampler node to plot a spectrum of the audio signal produced by the Stk Blit instrument.

Variable BPM

As discussed elsewhere, tempo changes are an important spice in the stew of life. This example is simple and crude but will hopefully set you on the road to time warping.

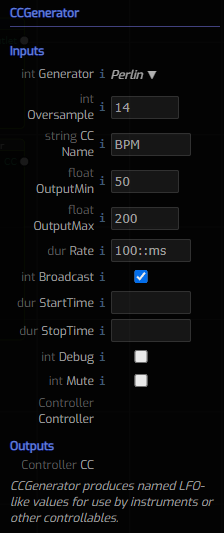
As you can see from the CCGenerator parameters at right, this is the parameter view of the node that produces a BPM control signal. The combination of its Rate and its Oversample parameters produces the frequency of our generated signal.

Here we employ Perlin Noise for our signal. Furthermore we impose no StartTime or StopTime on our signal generation time window.

Importantly we remap the approximately (-1, 1) range of Perlin noise onto an output range of (50, 200) and this means that we expect the BPM of our "composition" to randomly vary over that range.

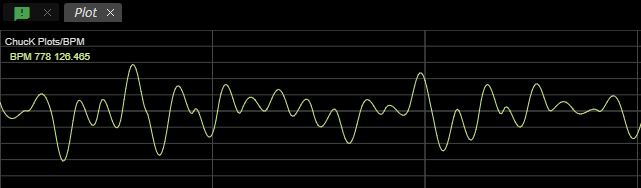
While performing, try modifying Oversample, Rate and the output range. while perusing the plot surface. Inspection of the downstream CCPlot node reveals that we've conveniently requested a plot surface name of BPM.

Here's a look at a plot of BPM. At the top peaks, the BPM is the highest value and the metronome clicks faster. Conversely the bottom peaks represent the slowest moments.

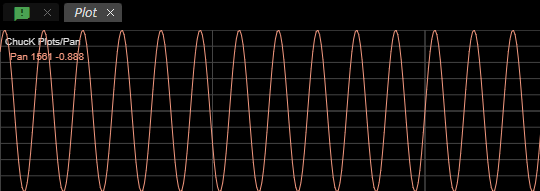
Non Variable Pan

The second CCGenerator node produces an uniform sine wave to modify the Pan parameter of the Chan0 node. Here's it's plot:

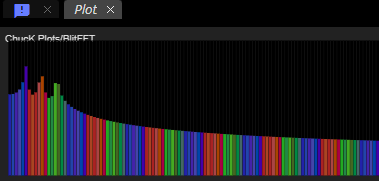
Blit Spectrum

Finally just for a sense of closure, here's a snapshot of the spectrum produced by the output of Stk Blit. We can infer from this plot that 3 harmonics are present in the audio synthesis.